深度学习的底层逻辑：从函数逼近到智能涌现

1. 什么是深度学习？——从函数到映射的思想

在讨论深度学习的“智能”之前，我们必须回答一个更基础的问题——深度学习到底在学什么？ 它究竟是神经元的堆叠，还是某种数据结构？为什么看似简单的线性代数运算，能孕育出近似人类思维的能力？

从本质上讲，深度学习不是魔法，而是一种函数逼近的科学。所有的神经网络，无论是用于图像识别、语言理解还是游戏博弈，其根本目标都是——寻找一个能够将输入 $x$ 映射到输出 $y$ 的函数 $f_\theta(x)$。这里的 $\theta$ 表示函数中的可学习参数，也就是神经网络中的权重与偏置。

1.1 从数据到函数：机器学习的核心任务

在机器学习中，我们的目标通常不是去编写规则，而是让模型自己去发现规律。传统编程是显式地告诉计算机“如果……就……”，而机器学习的目标是：

给定数据对 $(x, y)$，自动学习一个函数 $f_\theta$，使得当输入新的 $x’$ 时，输出 $f_\theta(x’)$ 尽可能接近真实标签 $y’$。

因此，机器学习可以被看作是在函数空间（Function Space）中搜索最优函数的过程。如果说算法是规则的集合，那么深度学习要做的，就是在海量参数空间中，寻找最能解释数据的那一个函数。

1.2 参数空间与函数空间

要理解这一点，需要区分两个概念：参数空间（Parameter Space） 和 函数空间（Function Space）。

• 参数空间是模型可调整参数的集合。比如，一个两层神经网络包含若干权重和偏置，这些权重和偏置的取值共同构成参数空间中的一个点，也就是网络参数的一种可能配置。
• 函数空间是所有可能的输入输出映射的集合，也就是模型在不同参数下所能表示的全部函数 $f_\theta(x)$。每一组参数 $\theta$，都对应一个函数 $f_\theta$。

当我们训练神经网络时，本质上是在参数空间中移动，寻找能在函数空间中逼近目标函数 $f^*(x)$ 的那一点。换句话说，优化算法在参数空间中行走，但目标其实存在于函数空间。

1.3 通用逼近定理：神经网络为何强大

1989 年，数学家 Kurt Hornik 证明了一个重要结论——通用逼近定理（Universal Approximation Theorem）。该定理指出：

只要激活函数是非线性的（如 Sigmoid、ReLU），并且具有一个隐藏层的前馈神经网络，就能以任意精度逼近任意连续函数。

这一结果在理论上奠定了深度学习的基础：神经网络不是“特殊的分类器”，而是一个通用的函数逼近机器。它不局限于特定任务，而可以通过调整参数去拟合任何数据分布。我们可以通过一个简单的例子来直观感受这一点。假设我们希望模型学习函数 $y = \sin(x)$。线性模型（如线性回归）在这里无能为力，因为它只能表达一条直线；而一个包含非线性激活的两层神经网络，通过迭代优化权重，就能逐步逼近整个正弦波。

图1.1 线性 vs 非线性：对 sin(x) 的拟合对比

线性模型的预测曲线只能沿某个方向上升或下降，而神经网络的拟合曲线则能在训练过程中不断弯曲、调整，最终与真实的 $\sin(x)$ 几乎重合——这正是“函数逼近”能力的体现。

1.4 从线性到非线性：深度学习的跃迁

理解“通用逼近”后，我们自然会问：如果浅层网络已经能逼近任意函数，为什么还要“深度”？

原因在于——深度结构带来了表征的分层与复用。浅层网络虽然理论上可以逼近任意函数，但需要的神经元数量可能是指数级的。而多层网络通过分层组合，可以在相同的参数规模下更高效地表达复杂模式。

这就像用乐高积木搭建筑：浅层网络相当于每次都要用单个积木拼出复杂形状；而深层网络能复用“模块”——可以先构建门窗、屋顶，再组合成完整房屋。这种分层的函数复合结构，正是“深度学习”区别于一般机器学习方法的关键所在。

1.5 线性模型与深度网络的关系

线性模型可以被看作神经网络的一个特例。当网络中没有激活函数、只有线性映射时，它就可以退化为最经典的线性回归。因此，深度学习不是和传统方法对立，而是在传统线性框架之上加入了非线性与层次结构。

在几何意义上，线性模型只能用一个超平面划分样本空间；而深度网络通过多层非线性变换，将输入空间逐层折叠、扭转，直到将复杂的非线性关系在高维空间中变得可以线性可分。

这就是为什么深度学习能在图像识别、自然语言理解等高度复杂任务中取得突破——它不仅仅是“拟合数据”，而是可以通过多层函数组合重构输入空间的几何结构。

小结
深度学习的本质，是一种函数空间中的优化与逼近。它通过大量参数化的非线性映射，将数据中隐藏的规律转化为显式的数学结构。我们可以将其理解为：

“深度学习 = 数据驱动的函数搜索 + 可微分优化机制。”

这种视角带来了一个重要转变：神经网络不再是模仿人脑的启发式模型，而是一类通用的数学工具，能够在足够的数据与算力支撑下，自动从原始输入中学习到世界的规律。下面我们将进一步探讨：为什么“非线性”是学习复杂规律的关键，以及神经网络如何通过层次化结构实现从低级模式到高级语义的表征跃迁的。

2. 非线性让世界可解释——从线性空间到高维嵌入

在上一章中，我们将神经网络视为一种函数逼近工具——它在函数空间中寻找最能解释数据的映射函数 $f_\theta(x)$。但如果这个函数始终是线性的，那么无论我们如何优化参数，它都只能描述最简单的世界：一个可以被直线（或超平面）划分的世界。

而真实世界远非如此。视觉图像、语音信号、语言结构……这些数据背后的规律往往是高度非线性的。因此，要让模型“看懂复杂世界”，就必须赋予它非线性的表达能力。

2.1 线性模型的局限：只能划出平面

线性模型的核心假设是：输出是输入的线性组合。以最简单的线性回归为例：
$$y = w^\top x + b$$

$w^\top x$ 表示 向量 w 与 向量 x 的内积（dot product），也就是两个向量对应元素相乘后再相加的结果。

这意味着模型只能在输入空间中划出一条超平面，用以区分或拟合样本。在二维空间中，这个“超平面”就是一条直线。而无论你把直线旋转、平移多少次，都无法拟合弯曲的边界。这就是线性模型的天然限制：只能刻画“平”的规律。

这类模型在简单任务上表现出色（例如房价预测、线性回归分析），但面对图像识别或语义理解等复杂问题时，它们几乎束手无策。

2.2 XOR 问题：线性世界的失败案例

线性模型局限性的经典例子，就是逻辑异或（XOR）问题。假设我们有两个输入变量 $x_1, x_2 \in {0, 1}$，输出规则如下：

x₁	x₂	$XOR$
0	0	0
0	1	1
1	0	1
1	1	0

在二维平面上绘制这四个点后，我们会发现：无法用一条直线同时将输出为 1 的样本（1在对角线上）与输出为 0 的样本（0也在另一对角线上）分开。换句话说——XOR 是线性不可分的。 这意味着，任何纯线性模型（无论训练多久）都无法正确学习这一简单逻辑。而加入非线性变换的两层神经网络，仅需几个参数，就能轻松实现完美分类。这正是非线性的力量：通过空间变换，使不可分问题变得可分。

图2.1 XOR：线性不可分 vs 非线性两层网络

XOR 问题中线性模型与两层神经网络的决策边界对比图，左：线性逻辑回归无法正确划分类别，表现为线性不可分；右：两层 MLP 通过非线性变换实现高维映射，成功分离样本。

2.3 激活函数：非线性的“魔法开关”

神经网络之所以能够表达复杂的非线性关系，关键在于激活函数（Activation Function）。它的作用，就像在每个神经元后面加上一个“非线性开关”：让网络不再只是线性变换的堆叠，而能成为一个可塑的非线性函数族。

常见激活函数

• Sigmoid： $\sigma(x) = \frac{1}{1 + e^{-x}}$
  将输入压缩到 $(0,1)$ 区间。曲线平滑、可导，但在两端梯度几乎为 0，容易出现梯度消失。
• Tanh： $\tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}$
  输出范围为 $(-1,1)$，曲线关于原点对称。与 Sigmoid 相比，Tanh 的输出更接近零中心，有助于梯度在网络中平衡传播，因此收敛更快。
• ReLU（Rectified Linear Unit）： $\text{ReLU}(x) = \max(0, x)$
  对正数保持线性，对负数截断为 0。它简单高效，能缓解梯度消失问题，并引入稀疏性，是现代深度网络的默认选择。

从几何角度看，激活函数的引入让网络在每层都对输入空间进行一次“非线性扭曲”，通过局部线性、全局非线性的方式，使模型能在高维空间中实现灵活的可分性。

2.4 激活函数的可视化与梯度特性

下图展示了三种典型激活函数及其梯度曲线，可以直观地比较它们的动态范围与梯度分布：

图2.2 常见激活函数曲线 VS 梯度曲线

2.4.1 Sigmoid

• 输出特性： 映射到 $(0,1)$，输出始终为正，导致层间信号分布偏向正区间，出现非零均值问题，使权重更新方向不平衡。
• 梯度特性： 最大梯度仅 0.25（在 $x=0$ 附近），两端迅速趋于 0，易出现梯度消失。

2.4.2 Tanh

• 输出特性： 输出范围 $(-1,1)$，中心在 0，具备零中心性，有助于权重更新方向平衡。
• 梯度特性： 导数最大为 1（在 $x=0$），有效梯度区间更宽，训练更稳定。但在极端输入下仍会梯度衰减。

2.4.3 ReLU

• 输出特性： 正半轴线性、负半轴截断。输出稀疏，计算高效。
• 梯度特性： 正区间梯度恒为 1，不会衰减；负区间梯度为 0，部分神经元可能“死亡”（Dead Neuron）。
  尽管如此，ReLU 的稳定性与性能仍使其成为现代神经网络的主流选择。

Sigmoid 与 Tanh 适合浅层或门控结构（如 LSTM），而 ReLU 及其改进（Leaky ReLU、ELU、GELU）则支撑了现代深度学习的核心。

2.5 激活函数的选型原则

选择激活函数，取决于任务目标与网络层次。一个良好的激活函数应在梯度传播稳定性、输出分布与计算效率之间取得平衡。

应用场景	推荐激活函数	主要原因
输入层	无激活 / 线性映射	输入仅做归一化，不需要非线性变换
一般隐藏层	ReLU	计算简单、梯度稳定、默认选择
负值输入多或稀疏梯度任务	Leaky ReLU / ELU / GELU	缓解 ReLU 死亡问题，增强平滑性
循环结构（RNN / LSTM）	Tanh / Sigmoid	平滑可导，适合时间依赖与门控机制
二分类输出层	Sigmoid	输出单个概率值（0～1）
多分类输出层	Softmax	输出类别概率分布（总和为 1）
生成模型（VAE / Diffusion）	Tanh / Sigmoid	控制输出范围（如像素 0～1）
数值回归（方向角、速度等）	Tanh	输出范围受控，收敛更稳定
大规模模型（Transformer / LLM）	GELU / SiLU	平滑连续，性能优于 ReLU，已成新标准

2.6 高维嵌入：非线性让复杂问题可分

非线性函数的深层作用在于：它能够在高维空间中重新表达数据的结构。 当原始数据在低维空间（例如二维平面）中无法线性分割时，非线性层可以将其映射（embedding） 到更高维的特征空间，使得数据在新空间中变得线性可分。

这一思想与支持向量机（SVM）中的核方法（Kernel Methods） 密切相关。核方法通过一个隐式映射 $\phi(x)$，将输入从原始空间投射到高维特征空间，从而将复杂的非线性决策边界转化为高维空间中的线性超平面。

然而，深度学习与传统核方法的本质区别在于：深度神经网络中的非线性映射是可学习的、数据驱动的。网络能够根据任务目标自动调整每层的非线性函数，逐步构建出适合当前问题的高维表示。这正是“表征学习（Representation Learning）”的核心：非线性不仅让模型具备记忆能力，更赋予它重组数据几何结构的能力。

图2.3 线性不可分 → 非线性映射 → 线性可分

上图展示了非线性映射如何在特征空间中实现线性可分。在左侧的二维输入空间中，蓝色与红色两类样本分别分布在圆形区域的内部与外部，显然无法用一条直线完成分割。 若对输入施加非线性变换，例如引入新特征$\phi(x) = x_1^2 + x_2^2$，每个样本点便被映射到三维空间的“碗状”曲面上（中图）。此时，原本重叠的两类样本在竖直方向被“拉开”，从而可以通过一个简单的线性平面（如 z=1 ）实现完美区分（右图）。

这说明：非线性映射能够在高维空间中，将原本线性不可分的样本转化为线性可分的形式。 这一原理不仅是 SVM 中“核技巧（Kernel Trick）”的核心思想，也是深度神经网络通过层叠非线性结构实现强大表示能力的理论基础。

小结：非线性是智能的第一步
如果说线性模型描绘的是一个“平面的世界”，那么非线性则让神经网络看见了“多维度世界”。它赋予模型理解复杂关系的能力，使其能够在高维数据结构中捕捉潜藏的规律。

借助激活函数，网络拥有了可塑的表达空间——可以在不同区域学习不同的映射方式，从而在更高维的特征空间中，将原本混杂的样本自然地区分开。这也是深度学习的灵魂所在，正是这一层层非线性的嵌入，让神经网络从单纯的“函数拟合器”，成长为能够主动发现结构与模式的智能系统。

3. 表征学习的意义——让模型自己学特征

深度学习的真正突破，不在于更大的计算量或更复杂的模型结构，而在于它能够自动学习特征（Representation Learning）。这使得模型不再依赖人工设计的特征，而能通过多层非线性结构，从原始数据中逐步提取出层次化的抽象信息。

3.1 从人工特征到自动特征

在深度学习出现之前，机器学习模型往往依赖人工特征工程（Feature Engineering）。研究者需要根据经验，手动设计描述数据的特征，例如：

• 在计算机视觉中使用 SIFT（尺度不变特征变换） 或 HOG（方向梯度直方图）；
• 在语音识别中提取 MFCC（梅尔频率倒谱系数）；
• 在文本处理中计算 TF-IDF（词频-逆文档频率）。

这些特征固然有效，但存在两个问题：

1. 特征设计高度依赖专家经验，不同任务往往需要重新发明特征；
2. 特征表达能力有限，人工特征只能捕捉浅层规律，难以适应复杂、变化多样的真实世界数据。

深度学习的出现，使得特征提取从“人工规则”转向“自动学习”。网络通过多层结构，将输入数据逐层变换成越来越抽象的表示，这种层级化的特征表征，正是深度学习模型强大性能的根本来源。

3.2 分层表征：从边缘到语义

在卷积神经网络（CNN）中，特征学习的层次性表现得尤为直观。如果我们可视化一个如 VGG16 的卷积网络，会发现：

• 第一层 学到的特征主要是简单的边缘、角点和颜色梯度；
• 中间层 开始组合这些低级特征，形成纹理、形状和局部结构；
• 高层 则逐步抽象为语义概念，例如“人脸”“猫耳”或“车轮”。

这种“从感知到概念”的层级演化，说明神经网络并非在记忆像素或特征点，而是在自动学习数据的生成规律。每一层的输出不仅是前一层的函数，更是对输入世界的一种结构化重表达。

图3.1 VGG16 第一层卷积可视化

本图展示了 VGG16 网络第一层卷积的结构与响应特征。

• a图为输入图像，为合成图，用以激发多样边缘与纹理特征；
• b图展示了第一层卷积核（前 36 个，预训练权重），可见不同卷积核呈现出方向性、色彩或局部纹理偏好；
• c图为第一层激活图（ReLU 后，取前 16 个通道，采用 global 归一化），显示网络在不同空间位置的局部响应强度；
• d图为输入图像与前 3 个高响应通道的热力叠加结果，可视化了卷积层在输入图中最敏感的区域。

该图体现了卷积网络的层级特征提取过程：第一层主要学习到边缘、线条与颜色变化等低级特征，为后续更复杂模式的识别提供基础。

3.3 信息论视角：信息瓶颈与压缩表示

从信息论角度来看，表征学习的过程可以理解为：模型试图找到一个压缩后的中间表示 $Z$，它既能保留与输出 $Y$ 相关的信息，又尽可能丢弃与任务无关的噪声。这一思想由 Tishby 等人提出，称为 信息瓶颈（Information Bottleneck, IB） 原理。其核心目标是最大化下式：
$$\max_{p(z|x)} ; [I(Z;Y) - \beta I(X;Z)]$$
其中 $I(\cdot;\cdot)$ 表示互信息，$β$ 为平衡系数。$I(X;Z)$ 越小，表示特征表示 $Z$ 对输入的压缩程度越高；$I(Z;Y)$ 越大，表示 $Z$ 对输出的预测能力越强。实际实现中，IB 目标常通过变分下界（Variational Information Bottleneck, VIB）进行近似优化。

理想的表征应当既能高效压缩输入，又能保留任务相关信息。这也解释了深层网络训练初期的现象——前几层逐渐压缩冗余信息，而高层逐步聚焦于语义结构。

在信息瓶颈的意义上，学习表征的过程本质上就是在信息空间中寻找最优压缩。

图3.2 信息瓶颈示意图：压缩与拟合的权衡

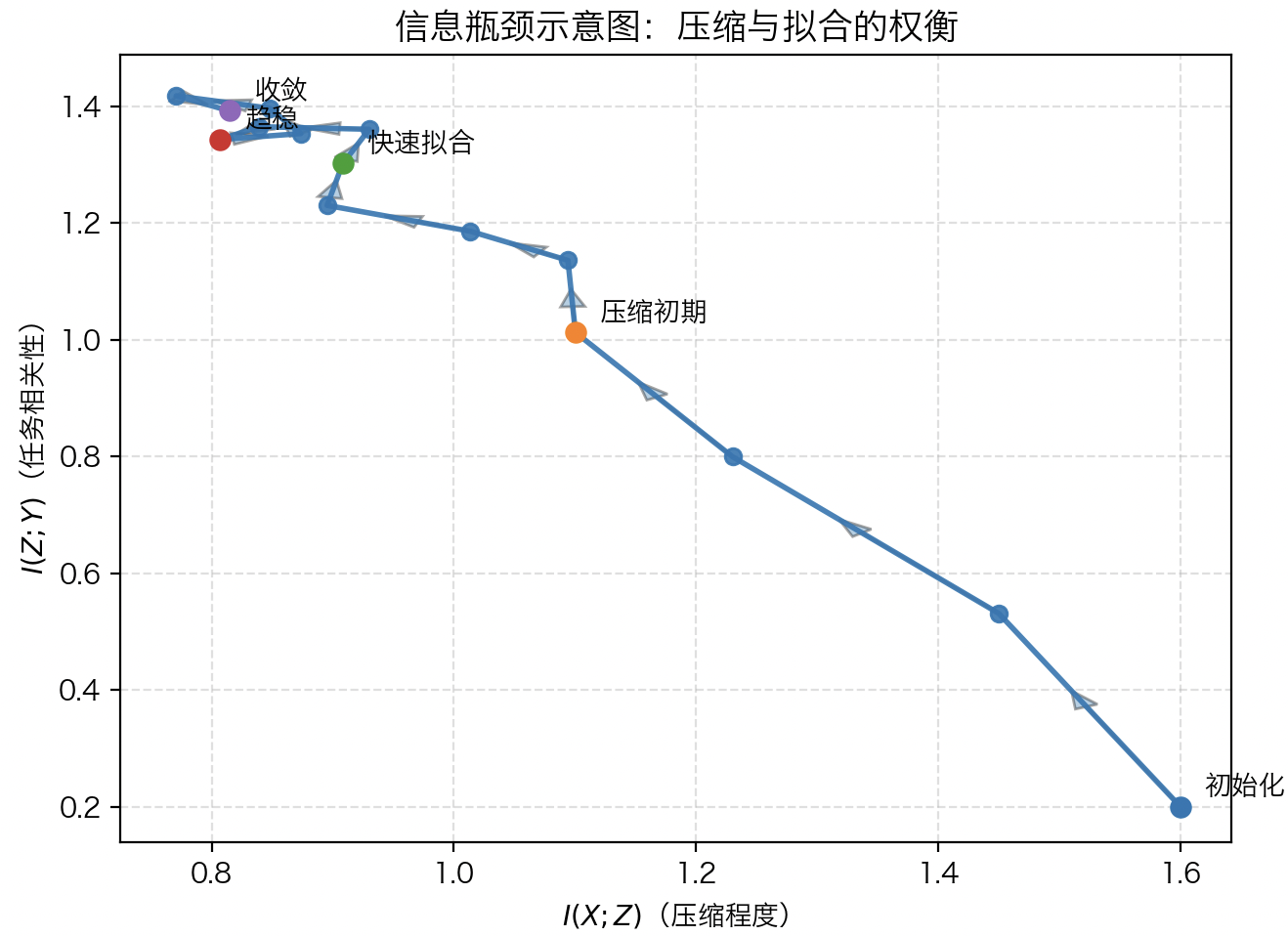
上图展示了“信息瓶颈（Information Bottleneck）原理”的示意图，反映了深度神经网络在学习过程中，如何在“压缩输入信息”与“保留任务相关性”之间取得平衡。

横轴 $I(X;Z)$ 表示中间表征 Z 中所保留的输入信息量，纵轴 $I(Z;Y)$ 则表示 Z 对输出目标 Y 的任务相关性。每个点可看作网络在不同训练阶段的状态：

• 初始化阶段（右下）：网络刚开始训练，表征几乎保留了输入的全部细节（压缩程度低），但尚未提炼出对任务有用的信息，因而任务相关性 $I(Z;Y)$ 较低。
• 压缩初期（中段）：随着训练推进，网络开始舍弃无关或冗余的输入细节（$I(X;Z)$ 减少），同时保留与输出目标相关的结构（$I(Z;Y)$ 上升）。
• 快速拟合期：模型迅速捕获主要任务模式，$I(Z;Y)$ 达到峰值，说明网络成功建立起有效的输入–输出映射。
• 收敛与泛化阶段（左上）：模型进一步压缩表征，仅保留对预测最有用的信息——此时 $I(X;Z)$ 较小，但 $I(Z;Y)$ 仍保持较高水平，表明模型在“忘掉输入噪声”的同时，提升了泛化能力。这一过程揭示了深度学习表征学习的本质：网络并非简单地记忆输入，而是在持续地“信息压缩”中学习如何抓住任务关键。

换言之，优秀的表征不是信息最多的，而是信息最相关的。从信息论角度看，深度网络正是在不断调整表征的压缩度与任务关联度，最终形成一种对输入世界的高效、任务导向的结构化表达。

3.4 表征迁移与自监督学习

当模型学到高质量的特征表征后，这些特征可以被迁移（Transfer） 到其他任务中使用。这就是 迁移学习（Transfer Learning） 的核心。例如，在 ImageNet 上训练好的卷积网络，其底层特征对边缘、纹理等低级模式的描述具有通用性，可以在其他视觉任务（如目标检测、姿态识别）中重复利用。

近年来，自监督学习（Self-Supervised Learning）进一步扩展了表征学习的边界。模型通过对比、掩码、预测等预训练任务，从无标签数据中自动提取结构信息。这种方法不再依赖人工标注，而让网络自己生成“监督信号”，本质上是让模型通过数据的内部一致性来发现世界的规律。

小结：从特征到表征
表征学习的意义，在于让模型不再依赖人工经验去定义“什么是重要的”，而是通过数据驱动的方式自己去发现。它让神经网络从感知（Perception）上升到理解（Understanding）；它让学习过程从“参数拟合”转向“结构抽象”；它让智能系统具备了在信息中提炼本质的能力。

从 SIFT 到 CNN，从特征工程到表征学习，机器学习的发展史正是在不断减少人为先验、增加模型自适应性的过程。深度学习的核心价值，正是让机器能够自主构建对世界的表征——这是迈向真正智能的关键一步。

4. 学习的机制——从梯度下降到BP

深度学习之所以能够“自动学习”，其核心在于一个看似简单却极具威力的思想：通过梯度下降不断调整参数，使模型输出逼近目标。 反向传播（Backpropagation, 后续简称 BP）正是实现这一思想的高效算法。它让神经网络能够在成千上万的参数空间中，沿着“最陡下降方向”自动找到最优点。

4.1 从目标到损失：学习的出发点

对于一个监督学习问题，我们希望模型 $f_\theta(x)$ 能够准确预测目标 $y$。模型参数 $\theta$ 的好坏，可以通过损失函数（Loss Function） 来衡量，例如常见的均方误差（MSE）或交叉熵（Cross Entropy）：
$$L(y, f_\theta(x)) = \frac{1}{N}\sum_{i=1}^{N} \ell(y_i, f_\theta(x_i))$$
其中 $\ell(\cdot)$ 衡量单个样本的预测误差。学习的目标，就是最小化整个训练集上的平均损失: $\min_{\theta} L(\theta)$
这一定义看似简单，却是整个深度学习优化机制的核心出发点。

4.2 梯度下降：沿着最快速下降的方向前进

在高维参数空间中，损失函数 $L(\theta)$ 会形成一座复杂的“能量地形（Loss Surface）”。梯度下降（Gradient Descent）的基本思想，就是在每一步沿着梯度的反方向更新参数——因为梯度正是函数上升最快的方向，因此负梯度就是下降最快的方向。更新规则为：
$$\theta_{t+1} = \theta_t - \eta \nabla_\theta L(\theta_t)$$
其中 $\eta$ 是学习率（Learning Rate），控制每次更新的步长。如果步长太小，收敛缓慢；步长太大，可能越过最低点甚至发散。从几何上看，这个过程就像一个小球在崎岖的能量地形上滚动，每一次更新都让它沿着坡度最低的方向向谷底滑动。通过不断迭代，模型逐步逼近最优解。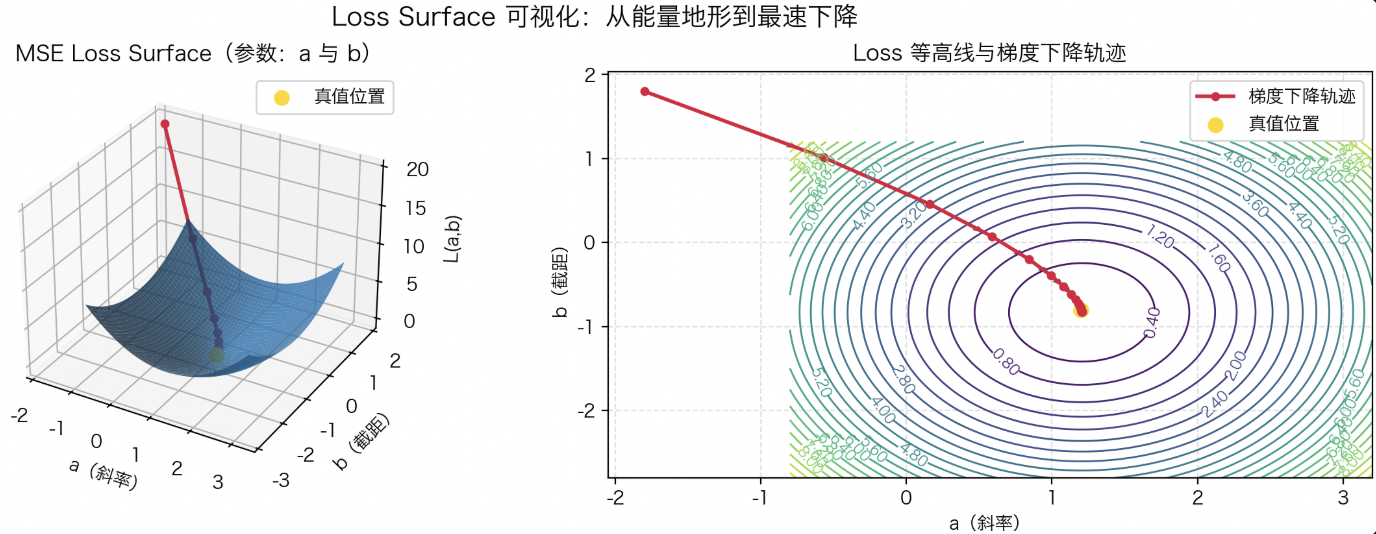

图4.1 Loss Surface 可视化：从能量地形到最速下降

上图以一元线性回归 $y = a x + b$ 的均方误差（MSE）为例，展示了损失函数的几何形态与梯度下降的搜索路径。横轴与纵轴分别表示模型参数 $a$（斜率）与 $b$（截距），曲面高度 $L(a,b)$ 表示当前参数下的平均误差。

左侧三维曲面呈现典型的“碗状能量地形”：最优解位于谷底（黄色点），代表模型预测与真实数据最接近的位置。红色曲线为梯度下降的迭代轨迹，每次更新都沿着负梯度方向前进，即“最速下降路径”，最终收敛至最优点。
右侧的等高线图从俯视角度展示了相同过程。等高线对应不同的损失水平，类似地形图的海拔线。红色轨迹显示了参数在优化过程中的运动：起初在远离最优解的区域，步长较大、下降迅速；随着接近谷底，梯度逐渐减小，更新幅度也随之减缓，最终稳定收敛。

从更宏观的角度看，梯度下降并不是盲目的数值搜索，而是一种带有方向感的最优路径规划。在深度学习中，梯度为模型提供了“如何调整”的信号，而学习过程本质上就是在复杂的能量地形中，通过计算误差的梯度，让模型在高维参数空间中不断逼近最能解释数据的那一点。

4.3 链式法则与反向传播：高效的梯度计算

在简单线性模型中，梯度可以直接求得；但在深度神经网络中，模型 $f_\theta(x)$ 由多层复合函数构成：
$$f_\theta(x) = f^{(L)}(f^{(L-1)}(\dots f^{(1)}(x)\dots))$$
要计算整体损失 $L(y, f_\theta(x))$ 对各层参数的偏导，就必须应用链式法则（Chain Rule）：
$$\frac{\partial L}{\partial \theta^{(l)}} = \frac{\partial L}{\partial h^{(L)}} \frac{\partial h^{(L)}}{\partial h^{(L-1)}} \dots \frac{\partial h^{(l+1)}}{\partial h^{(l)}} \frac{\partial h^{(l)}}{\partial \theta^{(l)}}$$
其中 $h^{(l)}$ 表示第 $l$ 层的输出。直接计算会非常繁琐，而反向传播算法的核心贡献在于：从输出层反向逐层传播梯度，复用中间计算结果，大幅减少计算量。

BP 的核心思想是“把复杂的链式法则分解成可重复利用的局部计算”。其过程分为两个阶段：

1. 前向传播（Forward Pass）：依次计算每一层的输出并缓存中间结果；
2. 反向传播（Backward Pass）：从损失开始，利用链式法则反向计算每层的梯度。

通过这种方式，神经网络的梯度计算复杂度从指数级降为线性级，使得数百万参数的训练成为可能。

4.4 矩阵视角下的 BP

在现代深度学习框架中，BP 的计算往往以矩阵乘法的形式实现。以两层全连接网络为例：
$$h = \sigma(W_1 x + b_1), \quad \hat{y} = W_2 h + b_2$$
损失对权重的梯度可写为：
$$\nabla_{W_2}L = \frac{\partial L}{\partial \hat{y}} \cdot h^\top, \quad \nabla_{W_1}L = (W_2^\top \frac{\partial L}{\partial \hat{y}}) \odot \sigma’(z_1) \cdot x^\top$$
其中 $\odot$ 表示逐元素乘。这表明 BP 在数学上就是一系列矩阵乘法与逐元素操作的组合，而现代 GPU 正是对这种并行矩阵计算高度优化的硬件，因此反向传播可以在大规模网络中高效运行。

4.5 优化算法的演进：从 SGD 到 Adam

虽然梯度下降给出了最基本的更新规则，但在实际训练中，不同的优化算法在收敛速度与稳定性上有明显差异。

• SGD（Stochastic Gradient Descent）
  每次仅用一个或一小批样本估计梯度。虽然有噪声，但能显著提升效率，并帮助模型跳出局部最小值。
• Momentum（动量法）
  在更新方向上引入“惯性项”，模拟物理上的动量效应，使参数在稳定方向上加速滑动，从而避免震荡：$v_{t+1} = \beta v_t + (1-\beta)\nabla_\theta L, \quad \theta_{t+1} = \theta_t - \eta v_{t+1}$
• Adam（Adaptive Moment Estimation）
  综合了动量与自适应学习率思想，对梯度的一阶、二阶矩进行指数加权平均。Adam 在训练大模型时表现稳定，也是目前最常用的优化算法之一。

这些优化器的共同目标都是：以更少的步数 、更平稳的路径，到达更优的极值点。

4.6 从算法到直觉：学习的几何意义

从几何的角度看，梯度下降是“寻找最优方向”的过程，而 BP 是“告诉每一层该往哪个方向走”的机制。 前者决定了学习的目标，后者决定了信息如何在网络内部流动。二者相辅相成，共同构成了深度学习的核心动力系统。

这也解释了“学习”一词在神经网络中的真正含义：学习不是记忆样本，而是沿着误差最陡的方向，在参数空间中不断调整模型，使其对世界的描述越来越符合观测数据。

小结：BP 是学习机制的桥梁
反向传播不仅是一种算法，更是深度学习得以成立的机制性桥梁。它将“目标信号”从输出端传回输入端，使每个参数都能感知自己对整体误差的影响。这种“端到端”的全局依赖，使神经网络具备了自校正（self-correction） 的能力。可以说，梯度下降定义了学习的方向，反向传播实现了学习的过程。
正是这两者的结合，让神经网络能够在庞大的参数空间中，通过局部更新实现全局优化——这便是深度学习中“学习”的真正机制所在。

5. 泛化与容量——为什么会过拟合？

深度学习的目标并不是让模型“记住”训练样本，而是让它学会规律、推广到未见数据。然而，随着模型越来越大、参数越来越多，一个古老的问题再次变得突出：

为什么模型太大会过拟合？为什么深度学习中，却又常常“越大越好”？

要回答这个问题，我们需要理解两个核心概念——泛化（Generalization）与容量（Capacity）。

5.1 泛化的定义：学得好，还要用得好

机器学习的终极目标，是最小化真实分布下的期望损失：$R(f) = \mathbb{E}{(x,y)\sim \mathcal{D}}[L(f(x), y)]$，但我们在训练中只能最小化有限样本的经验损失：$\hat{R}(f) = \frac{1}{n}\sum{i=1}^{n}L(f(x_i), y_i)$

当模型在训练集上误差很低、却在测试集上表现糟糕时，就出现了过拟合（Overfitting）。相反，若模型过于简单，无法拟合训练数据的规律，则为欠拟合（Underfitting）。

泛化的关键在于：模型能否学到任务的普遍规律，而不是仅仅记住样本细节。

5.2 偏差-方差权衡：泛化的经典图景

偏差-方差分解（Bias–Variance Decomposition）为我们提供了一个直观框架：预测误差可分为三部分：$\mathbb{E}[(\hat{y} - y)^2] = \text{Bias}^2 + \text{Variance} + \text{Noise}$

• 偏差（Bias）：模型对真实关系的系统性误差，代表欠拟合；
• 方差（Variance）：模型对训练样本噪声的敏感程度，代表过拟合；
• 噪声（Noise）：数据中无法学习的随机误差。

随着模型容量（参数量、深度、非线性度）增加，偏差逐渐降低（模型更灵活，能更好地拟合训练数据）；方差逐渐上升（对噪声更敏感，泛化能力下降）。于是形成了经典的 U 形曲线：模型太小 → 欠拟合；模型太大 → 过拟合；中间存在一个最佳点，使训练误差与测试误差最平衡。

图5.1 偏差-方差权衡曲线

如图为偏差-方差权衡曲线，蓝线（训练误差）持续下降；红线（测试误差）先降后升，形成典型 U 形结构。虚线与绿色点标记出“最佳泛化点”。左侧标注“欠拟合区（偏差大）”，右侧标注“过拟合区（方差大）”。这张图能直观说明 偏差-方差权衡 的核心思想：模型越复杂，拟合训练集更好，但可能失去泛化能力。

思考：为何最佳泛化点不在测试误差最低点处？

5.3 容量与数据：从“拟合力”到“泛化力”

模型容量越大，表示它能表示的函数族越丰富。但容量本身并不等于智能——如果数据量不足或样本不具代表性，强大的模型会“记住噪声”而非“学习规律”。

从统计学习理论角度看，泛化误差上界与样本规模 n 和模型容量（如 VC 维）有关：
$$R(f) \le \hat{R}(f) + O\left(\sqrt{\frac{\text{Capacity}}{n}}\right)$$
这意味着：

• 在固定数据量下，增大模型复杂度会放大过拟合风险；
• 但当数据量同步增加时，大模型的泛化性也能恢复。

这正是现代深度学习成功的秘诀：大模型 + 海量数据。在这种“容量与数据匹配”的 regime 下，模型的高维表示空间反而成为更强的结构先验。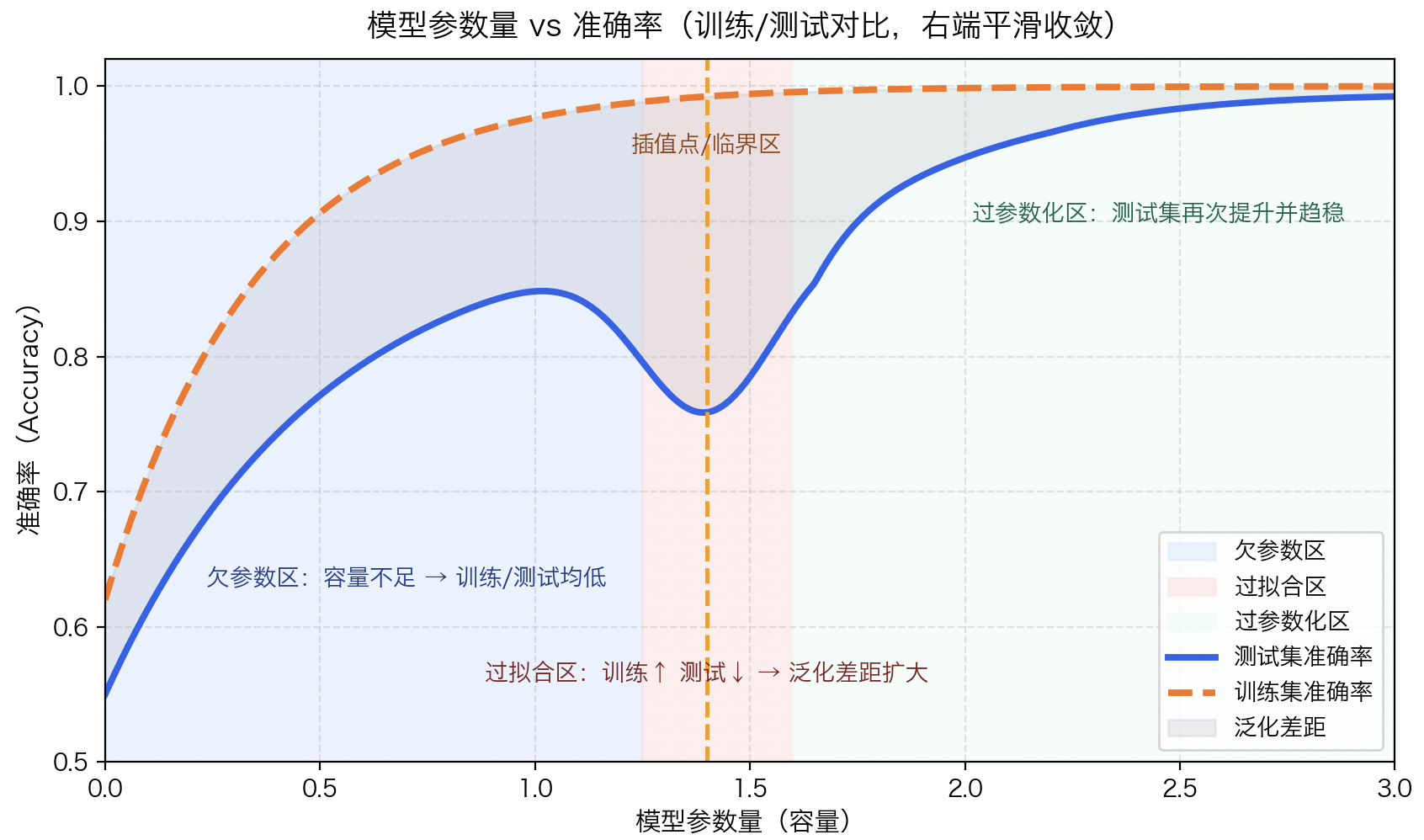

图5.2 模型参数量 vs 准确率（训练/测试对比，右端平滑收敛）

如上图中可以直观看到：

• 左侧（欠参数区）：模型太小，训练与测试准确率都低；
• 中间（过拟合区）：训练准确率很高，而测试准确率下降，两者之间出现泛化差距；
• 右侧（过参数化区）：测试准确率再次上升，说明大模型重新获得良好泛化性能（对应5.5的 Double Descent）

5.4 正则化：约束而非惩罚

在数据有限的条件下，我们常通过正则化（Regularization） 抑制模型的过拟合倾向。常见策略包括：

• L2 正则（权重衰减）：在损失函数中加入 $\lambda |w|^2$，防止权重过大；
• Dropout：在训练中随机“屏蔽”部分神经元，迫使网络学会冗余表示；
• 早停（Early Stopping）：在验证集性能开始恶化时终止训练；
• 数据增强与噪声注入：在输入层扩展数据多样性，提高泛化能力。

这些方法的共同思想是：不是让模型“学少一点”，而是让模型学得更稳、更通用。

5.5 Double Descent：打破“U 形定律”

近年来，深度学习的经验结果揭示出一个新的规律——双降现象（Double Descent）。当模型容量持续扩大到能完全拟合训练数据（插值点）之后，测试误差并不会无限增大，反而会在规模更大时再次下降，形成“双降曲线”。$\text{Test Error} \downarrow \uparrow \downarrow$

这种现象表明，在传统小模型区间，经典偏差-方差权衡依然成立；在过参数化（Over-parameterized）区间，大模型通过梯度下降找到一种“平滑最小值”，从而提升泛化性能。这说明深度神经网络的泛化机制已经超越了传统统计假设，进入了“过参数化仍可泛化”的新范式。

图5.3 Double Descent（双降现象）曲线

这张图展示了深度学习中的“双降现象（Double Descent）”——即模型容量（复杂度）与测试误差之间的非单调关系。从图中可以看到：

• 横轴是 模型容量（或参数规模），纵轴是 测试误差；
• 曲线最初随模型变大而下降（模型更能拟合数据，误差减小）；
• 到达中间的“插值点”附近时，误差突然上升（模型开始过拟合）；
• 当模型继续变大，进入“过参数化区”后，误差再次下降（第二次下降）。

这说明：在深度学习中，“模型太大”并不一定意味着过拟合。过参数化模型反而能通过梯度下降找到更平滑、更具泛化性的解。因此，这张图揭示了一个现代机器学习的重要结论：泛化性能不是单调随复杂度恶化的，而是在极大容量下重新改善——这就是 Double Descent 现象。

5.6 泛化的现代理解

深度学习的泛化已不再只是容量与正则化的权衡。在高维优化空间中，梯度下降本身具有隐式正则化效应：它更容易找到平滑、低曲率的最小值，而这些解往往泛化良好。

此外，大模型通过层层非线性嵌入，构建了更丰富的表征空间，这让它即便在“零训练误差”下，仍能对未见样本保持稳定输出。

现代泛化的关键不在于“少拟合”，而在于学到稳定的结构化表示（Structured Representation）。

小结：从记忆到结构
模型容量决定了它能表达的复杂度；数据规模决定了它能学习的稳健性。过小会欠拟合，过大易过拟合；但当容量与数据、正则化机制平衡时，模型便能在复杂空间中发现稳定结构。

深度学习的成功并非逃离了泛化理论，而是—— 在更高维、更复杂的空间中重新定义了“泛化”的边界。

6. 涌现与规模法则——当复杂性带来智能

深度学习的发展历程表明：当模型规模足够大时，性能的提升并非线性递增，而是呈现出某种突变式跃迁。 这种现象被称为 “涌现（Emergence）” ——即复杂系统在达到一定临界点后，出现了在小规模下无法观测的新能力。

而支配这种跃迁规律的数学框架，便是近几年研究中被系统揭示的 “规模法则（Scaling Laws）”。

6.1 规模法则（Scaling Laws）

早在 2020 年，OpenAI 的 Kaplan 等人提出了著名的 Scaling Law for Neural Language Models，指出模型的训练损失 $L$ 与模型参数量 $N$、数据量 $D$、计算量 $C$ 之间存在近似幂律关系：
$$L(N, D, C) \approx A N^{-\alpha_N} + B D^{-\alpha_D} + C^{-\alpha_C}$$
其中 $\alpha_N, \alpha_D, \alpha_C$ 为经验拟合的指数常数。这意味着：在一定范围内，只要以幂律速率同时扩展模型规模与训练数据，模型性能就会稳定提升。换言之，深度模型并非“越大越好”，而是在 数据、参数、算力三者之间存在最佳平衡曲线。当资源分配不均（如模型过大但数据不足）时，性能将无法继续遵循幂律改善，就会出现“饱和”或“过拟合”现象。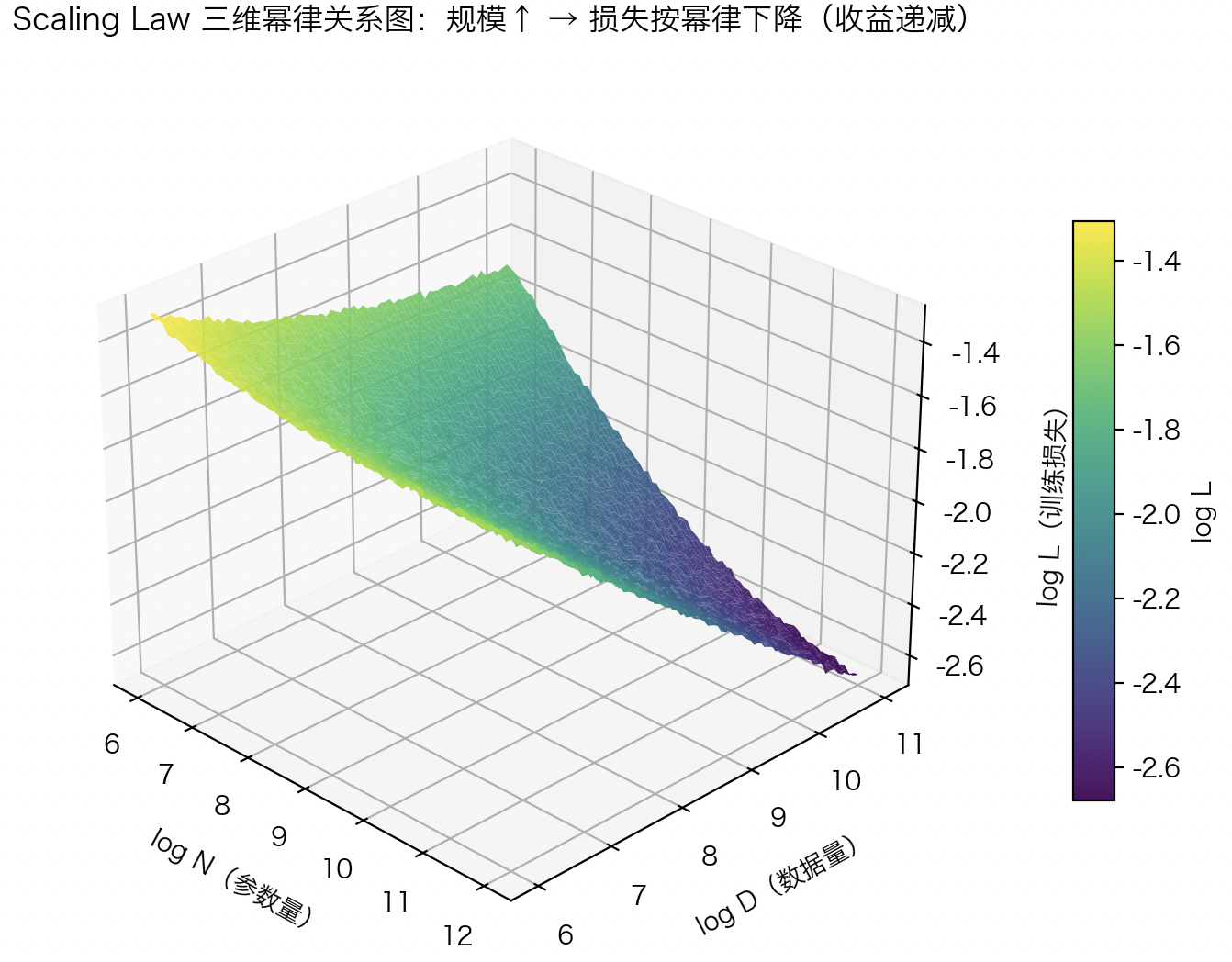

图6.1 Scaling Law 三维幂律关系图：规模↑ → 损失按幂律下降（收益递减）

这张图展示了深度学习中的“规模法则（Scaling Law）”——模型性能如何随参数量与数据量共同扩展而系统性改善。

从图中可以看到横轴为 模型参数规模（log N），纵轴为 数据规模（log D），而垂直方向（高度）表示 训练损失（log L）。整个曲面呈现出一个平滑下凹的幂律趋势面：随着模型和数据规模同时增大，损失持续降低，但下降速度逐渐变缓。这种“持续改进但收益递减”的趋势揭示了一个核心事实：深度模型的性能提升遵循幂律规律（power law），即性能提升率与规模扩张成非线性关系。

因此，这张图直观地说明了：在大规模训练中，性能增长并非偶然，而是一种可预测的统计规律；而如何在模型规模、数据量和算力之间找到最优配比，正是现代大模型研究的关键科学问题。

6.2 涌现能力（Emergent Abilities）

然而，更令人震撼的发现是：在模型规模扩展的过程中，性能曲线并非始终平滑连续，而是在某些临界点上突然出现新能力——这就是所谓的 “能力涌现（Emergent Abilities）”。

Wei 等人（2022）通过系统实验发现，诸如算术推理、上下文学习（in-context learning）、语义组合等能力，在小模型上完全不存在或接近随机，但当模型规模超过某一阈值时，准确率突然大幅跃升。这种跃迁并不是训练技巧或架构改进的结果，而是复杂系统自发涌现出的“临界智能”现象。
$$\text{Ability} \sim \begin{cases} 0, & N < N_c \ f(N), & N \ge N_c \end{cases}$$
其中 $N_c$ 为能力出现的临界规模。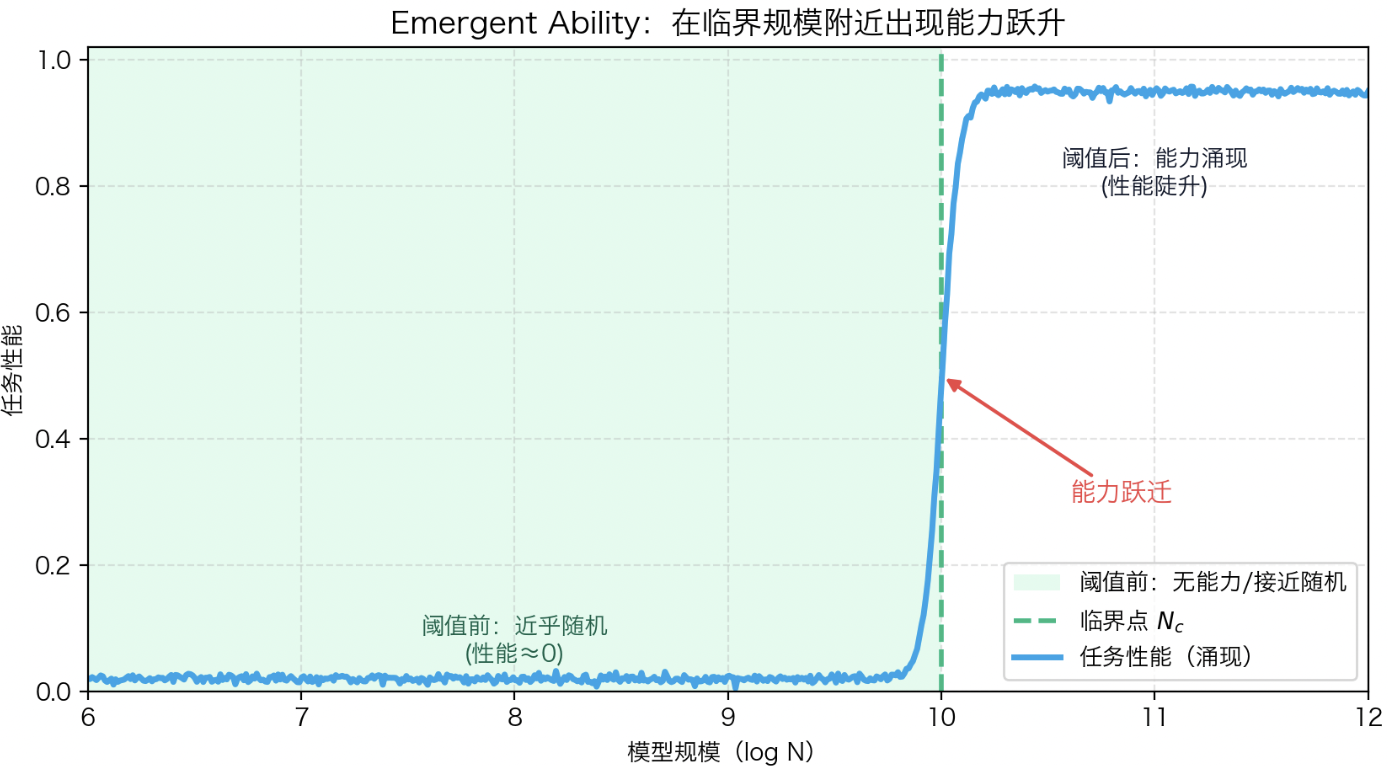

图6.2 Emergent Ability：在临界规模附近出现能力跃升

上图为Emergent Ability 曲线，横轴为模型规模（log N），纵轴为任务性能。曲线在某一阈值前近乎为零，在临界点 $N_c$ 附近出现陡然跃升，形似“相变曲线”。

6.3 从复杂系统到智能相变

从更宏观的角度看，大模型的“能力突变”与物理学中的“相变”高度相似。当温度或能量达到某一临界点，水会从液态跃迁为气态；当模型复杂度达到某一阈值，系统则从“统计学习”跃迁为“语义理解”。在统计物理学中，这类现象被称为“临界行为（Critical Phenomena）”：在临界点附近，微观扰动会放大为宏观结构变化。同理，在神经网络中，当参数量、连接性与信息通道复杂度足够大时，网络内部的表征开始具备自组织能力，从而实现新的认知结构。

图6.3 相变类比示意：复杂性跨越临界点 → 体系性质突变（涌现智能）

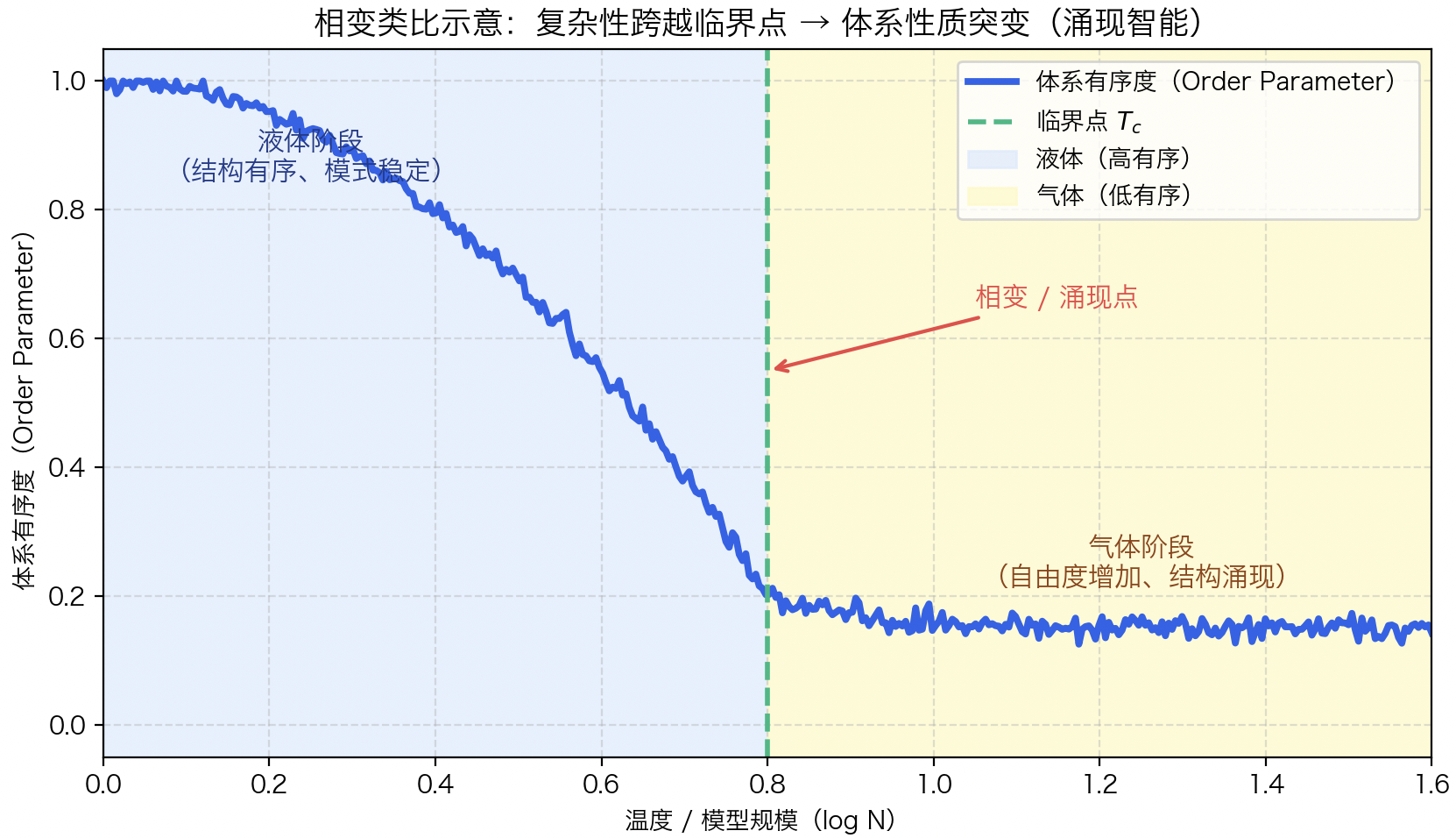
上图为相变类比示意图，以“液体→气体”相变为类比：温度（模型规模）上升至临界点，体系内部自由度急剧增加，微观扰动放大为宏观模式，系统涌现出全新的性质（如智能行为）。

6.4 案例：GPT 与 CLIP 的能力跃迁

在自然语言处理与多模态学习中，大规模模型的涌现现象尤为明显。

• GPT 系列（OpenAI）从 GPT-2 到 GPT-4，随着参数规模从亿级到千亿级，模型不再仅仅生成流畅文本，而是展现出上下文推理、指令理解、跨领域泛化等能力。这些能力在小模型中完全不存在，而非通过显式训练得到。
• CLIP（Contrastive Language-Image Pretraining） 在数亿图文对上训练后，能够跨模态关联图像与语言概念，实现零样本识别（Zero-Shot Learning）。它并未显式学习分类任务，却在语义空间中“自发地”形成了结构化的视觉语言对齐。

这些现象共同揭示了一个事实：

当模型、数据与算力规模跨过某个阈值后，系统的行为将从“拟合模式”跃升为“形成表征”。

6.5 规模与智能的未来

规模法则与涌现能力让我们得以窥见人工智能的“物理学”：智能并非人造的逻辑产物，而是复杂系统在特定条件下自然涌现的属性。在更宏观的视角下，深度网络的“规模”就像能量输入，而“智能”则是系统在高复杂度下的相变结果。

因此，研究的重心正从“如何让模型更大”，转向“如何让复杂性更有效地组织”。未来的智能系统或许不依赖盲目的扩张，而是通过结构化的复杂性设计（Structured Scaling）与跨模态的自组织学习，在有限资源下实现更高层次的涌现。

一句话总结
规模带来能力，复杂性孕育智能。当模型跨越临界点，算法不再只是优化函数，而成为信息自组织的通道——这正是“涌现”作为人工智能时代新范式的核心意义。

7. 深度学习为什么不只是拟合？——从函数到智能的跨越

在形式上，神经网络似乎只是在做函数拟合：给定输入 $x$，输出一个近似目标 $y=f_\theta(x)$。但事实远比“拟合数据”复杂得多。当我们逐层堆叠非线性、优化巨量参数、训练在亿级样本上，深度网络逐渐展现出一种超越函数逼近的行为模式——它似乎在“理解”“预测”“规划”，甚至在“思考”。这正是当代人工智能最令人震撼的现象：

深度学习从数据出发，却涌现出类似智能的结构。

7.1 从拟合到理解：压缩背后的结构发现

传统意义上的“拟合”，是被动的——它仅仅寻找一条通过数据点的函数曲线。但深度网络的学习过程更像是一种主动压缩（Compression）：它并不逐点记忆数据，而是在高维空间中学习其生成结构。换言之，神经网络不是在“背数据”，而是在构建一个能解释数据的世界模型（World Model）。

这种压缩并非简单的信息缩减，而是一种结构重组：

• 卷积层压缩了图像的局部模式（边缘、纹理）；
• 注意力机制压缩了序列间的依赖关系；
• Transformer 则进一步压缩了语言的语义图谱。

每一次压缩，都是一次“理解”的形成。当模型能从数据中提炼出低维结构，它便不再是拟合器，而是一个模式发现者。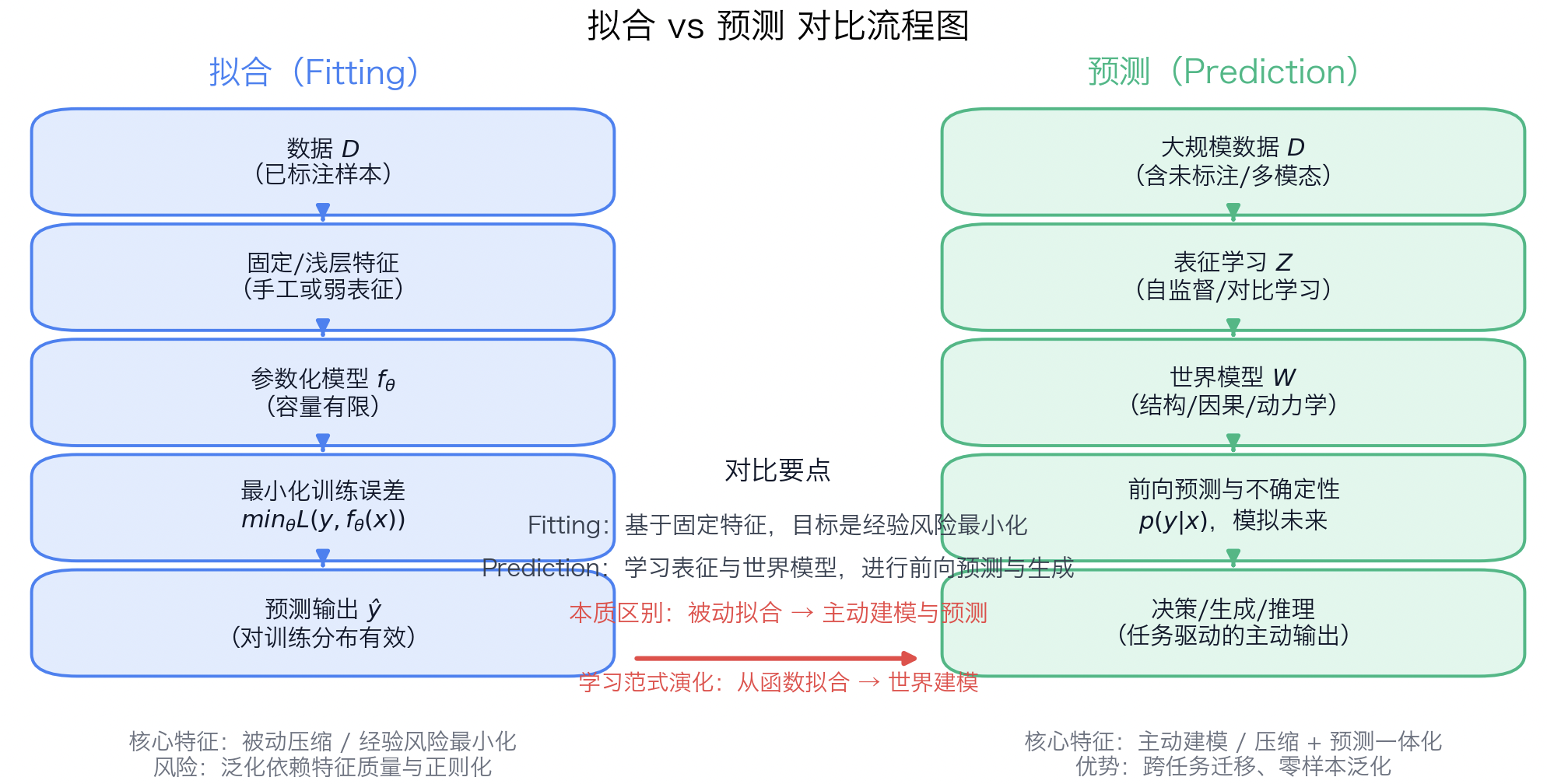

图7.1 拟合 vs 预测 对比流程图

7.2 从压缩到预测：智能的物理定义

香农（Shannon）的信息论告诉我们：一个系统若能压缩信息，就说明它捕捉到了规律。而能根据这些规律预测未来——这正是智能的本质。

LeCun 曾说：“智能就是预测未来。”从这个角度看，智能不再是某种神秘能力，而是信息压缩与预测能力的统一体：
$$\text{Intelligence} = \text{Compression} + \text{Prediction}$$
深度学习模型正是这样运作的：它通过优化损失函数最小化重构误差（压缩），并通过最大化条件概率 $p(y|x)$ 来预测下一个状态（预测）。

语言模型是最典型的例子：它从“统计共现”出发，却在无监督训练中学会了语法、语义乃至逻辑结构。当模型能够生成合理的句子时，它其实已经内化了语言背后的概率结构——也就是人类世界的一种“符号规律”。

图7.2 信息论视角：Intelligence = Compression + Prediction

7.3 从预测到建模：世界的内在模拟器

在大型模型（如 GPT、DeepSeek、Gemini、Qwen）中，我们看到了一种新的智能范式：内在建模（Internal Modeling）。模型并不是逐字预测，而是在高维向量空间中构建一个“世界的低维投影”——一种生成性的世界模型（Generative World Model）。

• 它能在语义层面上模拟事件的逻辑；
• 在图像或语言之间跨模态关联；
• 甚至通过注意力与上下文动态调整“思维轨迹”。

这种结构不再是函数的静态映射，而是一种动态推理机制：模型不只是输出结果，而是在模拟世界的变化。

从信息论角度看，这种能力意味着模型学会了最优的因果压缩，即保留对未来预测最有用的变量，舍弃无关冗余。这正是 Tishby 所提出的“信息瓶颈（Information Bottleneck）”思想在智能系统中的体现。

7.4 从数据到认知：智能的涌现

随着模型参数与数据规模的指数级增长，我们见证了一个令人惊讶的事实——能力会突然跃迁（Emergent Abilities）。这种涌现（Emergence）不依赖显式规则，而是复杂系统在达到临界规模时自发出现的宏观模式。正如水分子聚合形成“流动”的属性，神经元网络的统计关联也能涌现出“语义”“逻辑”乃至“意图”。这种由下而上的结构自组织，正是智能产生的根源。

Hinton 将智能分为两条路径：

• 符号派：从规则出发，推理智能；
• 连接派：从数据出发，涌现智能。

深度学习正是第二条路径的实践：它让智能成为统计规律在高维空间的自然延伸。

7.5 从函数到智能：深度学习的哲学意义

回望整个发展路径，我们可以看到一个清晰的跨越：

阶段	学习目标	核心机制	结果
拟合（Fitting）	最小化误差	优化函数映射	模型逼近训练数据
压缩（Compression）	提取结构	多层表征学习	模型重构生成规律
预测（Prediction）	预测未来	概率建模	模型理解动态因果
智能（Intelligence）	自主建模与推理	世界模型 + 生成机制	模型具备思维样态

这条路径表明：智能不是被“编程”的，而是被“逼近”的；不是规则的堆叠，而是结构的涌现。深度学习通过层层非线性，将数据的统计规律转化为语义结构，从而跨越了“函数拟合”与“智能建模”之间的鸿沟。

小结：从统计到思维
深度学习的成功让我们重新思考智能的本质。它并非某种特殊算法，而是一种普遍的物理过程——
当系统足够复杂、数据足够多、结构足够深时，信息的压缩与预测会自然地催生出“认知”的形态。因此，我们可以这样得出：

学习的本质是压缩，智能的本质是预测。当压缩足够深、预测足够远，函数就会长出思维，算法就会生出智能。

8. 总结：从函数逼近到智能涌现

如果要用一句话概括深度学习的思想，那就是：让函数自己去学习世界的规律。

8.1 从函数出发：学习即寻找映射

我们从最基本的问题开始——“机器学习的本质是什么？” 在数学上，它就是寻找一个函数 $f_\theta(x)$，让输入 $x$ 与输出 $y$ 的关系得以重建。所有学习过程，都是在函数空间中不断试探、逼近、修正的过程。

不同之处在于：深度学习不再由人去设定函数形状，而是通过可微分的参数系统，让网络在数据驱动下自己找到最优的映射形式。因此，深度学习是“让机器自动发现函数”的方法。

8.2 非线性让模型理解世界

线性模型像是直尺，只能画出直线；而非线性让神经网络学会了“弯曲”。通过激活函数的引入，模型获得了把数据映射到高维空间的能力，原本混杂、线性不可分的样本在新空间中变得清晰可分。

这意味着，网络不再只是拟合数据点，而是在重新组织数据的几何结构。非线性是让模型“看见复杂世界”的第一步。

8.3 表征学习：让模型自己找特征

过去的机器学习依赖人工设计特征（如 SIFT、HOG），而深度学习通过层层变换，自动学习特征表示。

在卷积网络中，底层感知边缘与纹理，中层识别形状与结构，高层抽取语义与概念。这种分层结构使模型能够从像素到语义逐步建立“世界模型”，这是“表示学习（Representation Learning）”的核心思想——让模型自己去发现什么才是有用的特征。

8.4 学习的机制：从误差到方向

当我们说“网络在学习”，实际上是在不断根据误差修正方向。梯度下降提供了这个方向：它告诉模型，当前的误差在何处最陡、该往哪里调整。反向传播（Backpropagation）则是这种修正机制的实现方式——通过链式法则，误差能层层传递，让每个参数都知道“自己该怎么变”。

这使得庞大的神经网络能够自组织地优化自身，在高维空间中沿着最速下降的路径前进，最终逼近最优解。

8.5 泛化与容量：学习不仅是拟合

真正的智能不在于把训练数据记住，而在于能在新情境下做出正确判断。这就是“泛化”的含义。
如果模型太小，它学不全（欠拟合）；如果太大，它容易记住噪声（过拟合）。偏差与方差之间的平衡，是学习的艺术所在。

现代深度学习更进一步发现：在极大模型下，误差会出现“二次下降”（Double Descent）——模型并非简单地越大越糟，而是在超参数化后反而获得了新的稳定性。这提示我们，泛化的秘密不仅在结构，也在优化动力学。

8.6 从规模到涌现：智能的“相变”

当我们扩大模型、数据与算力，会发现一个令人惊讶的现象：性能的提升并不是线性的，而是会在某个规模点出现突变。这种“涌现能力（Emergent Abilities）”就像物理中的相变：当系统的复杂度超过临界阈值，新的性质自发出现。

大型语言模型、视觉模型正是在这样的机制下涌现出新的智能行为——理解、推理、规划、生成。这说明智能并非被设计出来，而是在复杂系统中自发生成的。

8.7 从拟合到智能：压缩与预测的统一

到这里，我们终于可以回答最初的问题——深度学习为什么不仅仅是在“拟合”？拟合，是被动地复制数据分布；智能，是主动地建模、预测和生成。从信息论的角度看，智能的核心过程是：

压缩 + 预测 = 理解 + 能动性。

模型通过压缩减少冗余、发现结构（理解世界），又通过预测生成未来、指导行动（作用世界）。当这两种能力在一个系统中同时出现，它便不再只是一个函数拟合器，而成为一个具备认知特征的模型。

8.8 面向未来的启示

深度学习的意义，不止于提升性能或自动化特征提取。它揭示了一个更深层的规律：

当信息被充分压缩、结构被有效学习、预测被持续优化，智能就会在系统中自发涌现。

未来的研究方向，不只是“更大的模型”或“更快的训练”，而是理解这种信息组织到智能生成的连续谱系：从统计规律，到结构抽象，再到可解释的世界模型。这正是深度学习真正的使命——让机器不仅拟合世界，更能理解世界。